思想
排序算法
冒泡排序
- 比较相邻的元素,如果第一个比第二个大,就交换他们的位置
- 对每一组相邻的元素做相同的工作,直到得出第一个最大值
- 重复上述步骤,每次比较次数-1,直到不需要比较
c++
#include<iostream>
using namespace std;
int main()
{
int arr[] = {9,7,6,5,1,2,8,4,60,40,50,23,98,52,78,65,52};
int n = sizeof(arr)/sizeof(arr[0]);
for(int s = 0;s < n - 1;s++)
{
for(int i = 0;i < n -s- 1;i++)
{
if(arr[i] > arr[i+1])
{
int temp = 0;
temp = arr[i+1];
arr[i+1] = arr[i];
arr[i] = temp;
}
}
}
for(int j = 0;j < n;j++)
{
cout<<arr[j]<<endl;
}
return 0;
}快速排序
通过一趟排序将待排记录分隔成独立的两部分,其中一部分记录的关键字均比另一部分的关键字小,则可分别对这两部分记录继续进行排序,以达到整个序列有序.主要采用
分治法和挖坑填数等方法,分治法就是大问题分解成各个小问题,堆小问题求解,使得大问题得以解决.
python
def quicksort(arr):
if len(arr) <= 1:
return arr
pivot = arr[len(arr) // 2]
left = [x for x in arr if x < pivot]
middle = [x for x in arr if x == pivot]
right = [x for x in arr if x > pivot]
return quicksort(left) + middle + quicksort(right)
print(quicksort([3,6,8,10,1,2,1]))分数的处理
求两个数的最大公约数
- 辗转相减法
c++
while (a!=b)
{
if(a > b)
{
a = a - b;
}
else
{
b = b - a;
}
}- 欧几里得法
c++
while (a!=b)
{
c = a;a = b % a;b = c;
}牛顿迭代法求近似解
用于求一元方程的解
牛顿迭代法使用函数的泰勒级数的前面几项来寻找方程的根.
- 先猜测一个初始值 x₀;
- 在函数 f (x) 上找到点 (x₀, f (x₀)) 处的切线;
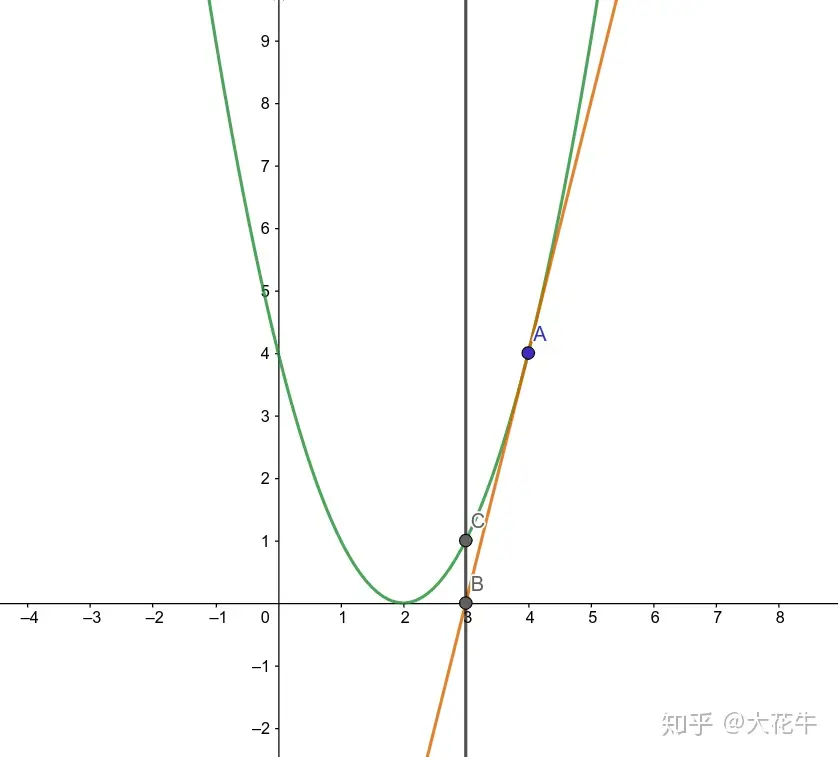
- 切线与 x 轴的交点作为新的猜测值 x₁;
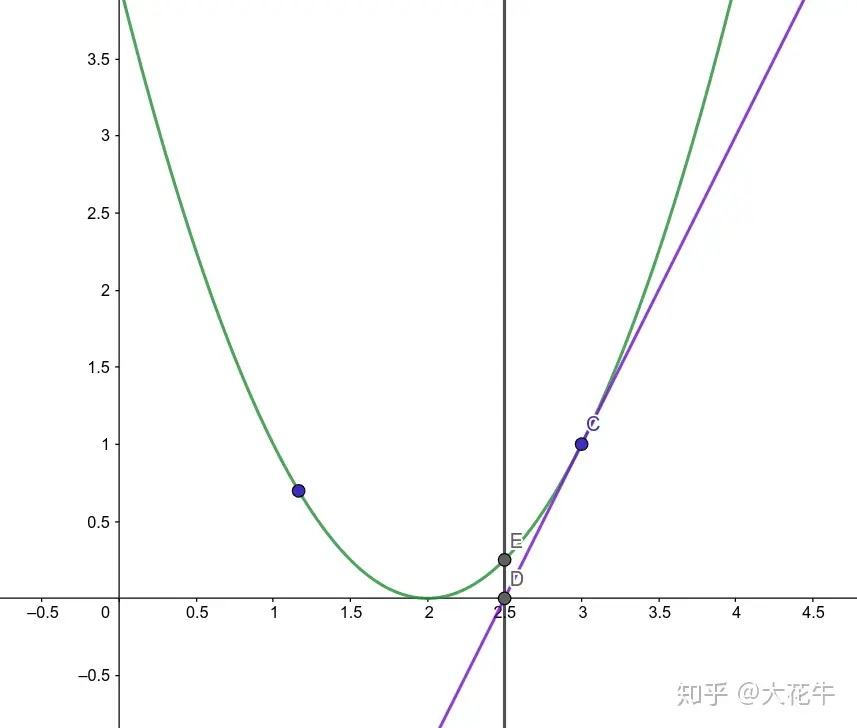
- 重复步骤2和步骤3,直到满足所需的精度或达到最大迭代次数.
- 注意多个输入的时候记得重新初始化值
递归算法
- 假设有一个函数f()可以解决问题,接下来的问题,这个函数长什么样
- 找到
fn()与fn-1()之间的关系 - 确定
f()的参数 - 分析并写出边界条件
**带有记忆的递归函数 **:用于提升递归的效率,减少深层次的递归
逆波兰表达式
总时间限制:
1000ms
内存限制:
65536kB
描述
波兰表达式是一种把运算符前置的算术表达式,例如普通的表达式2 + 3的波兰表示法为+ 2 3.波兰表达式的优点是运算符之间不必有优先级关系,也不必用括号改变运算次序,例如(2 + 3) * 4的波兰表示法为* + 2 3 4.本题求解波兰表达式的值,其中运算符包括+ - * /四个.
输入
输入为一行,其中运算符和运算数之间都用空格分隔,运算数是浮点数.
输出
输出为一行,表达式的值. 可直接用printf("%f\n", v)输出表达式的值v.
样例输入
* + 11.0 12.0 + 24.0 35.0样例输出
1357.000000提示
可使用atof(str)把字符串转换为一个double类型的浮点数.atof定义在math.h中. 此题可使用函数递归调用的方法求解.
c++
#include <iomanip>
#include <iostream>
#include <string>
using namespace std;
double calulate() {
string temp;
cin >> temp;
if (temp == "+") {
return calulate() + calulate();
} else if (temp == "-") {
return calulate() - calulate();
} else if (temp == "*") {
return calulate() * calulate();
} else if (temp == "/") {
return calulate() / calulate();
} else {
return stod(temp);
}
}
int main() {
double ans = 0;
ans += calulate();
cout << fixed << setprecision(6) << ans << endl;
return 0;
}深度优先搜索(DFS)
Depth-First Search
- 适合搜索全部的解
- 首次找到的不一定是最优解
- 空间复杂度低(和深度有关)
- 对每一个可能的分支路径深入到不能再深入为止,并且每个节点只能访问一次
c++
/*
关于输入
输入数据第一行两个整数n,m(1<=n,m<=100),表示照片的长和宽.
接下来n行,每行都有m个用空格隔开的整数(0或者1),表示这一照
片行的状态(有无细菌).
关于输出
输出一个整数,表示该张照片中菌落数量
例子输入
3 5
0 0 1 0 1
0 1 0 1 1
1 1 0 0 1
例子输出
3
*/
#include <iostream>
using namespace std;
#define MAXN 105
int map[MAXN][MAXN] = {}; // 用来记录细菌是否存在
int checkmap[MAXN][MAXN] = {}; // 用来标记该细菌是否被遍历过
int n = 0, m = 0, sum = 0; // n和m表示矩阵的高宽,sum用于记录连通块的个数
void dfs(int i, int j) // 深度优先搜索函数
{
if (map[i][j] && !checkmap[i][j]) {
checkmap[i][j] = 1; // 标记这个位置被遍历过了
map[i][j] = sum;//用于修改对应位置的记号
// 四个方向搜索
dfs(i - 1, j);
dfs(i + 1, j);
dfs(i, j - 1);
dfs(i, j + 1);
}
}
int main() {
cin >> n >> m;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
cin >> map[i][j];
}
}
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
// cout<<map[i][j]<<endl;
if (map[i][j] && !checkmap[i][j]) {
sum++;
dfs(i, j);
}
}
}
cout << sum << endl;
// for (int i = 1; i <= n; i++) {
// for (int j = 1; j <= m; j++) {
// cout<<map[i][j]<<' ';
// }
// cout<<endl;}
return 0;
}c++
/*
下楼问题:
u 从楼上走到楼下共有h个台阶,每一步有3种走法:
走1个台阶;走2个台阶;走3个台阶.问可以走出多
少种方案?将所有的方案输出
*/
#include <iostream>
using namespace std;
int take[99];
int num = 0; // num表示解决方案的总数
void trys(int i, int s) { // i表示所剩台阶数
for (int j = 3; j > 0; j--) { // 枚举第s步走的台阶数j
if (i < j) // 如果所剩台阶数i小于允许走的台阶数j
continue;
take[s] = j; // 记录第s步走j个台阶;
if (i == j) { // 如果已经走完全部台阶;
num++; // 方案数加1
cout << "solution" << num << ": ";
for (int k = 1; k <= s; k++)
cout << take[k];
cout << endl;
} else
trys(i - j, s + 1); // 尚未走到楼下
}
}
int main() {
int h = 0;
cout << "how many stairs : ";
cin >> h;
trys(h, 1); // 有h级台阶要走,从第一步开始走
cout << "there are " << num << " solutions." << endl;
return 0;
}回溯算法
回溯需要还原节点状态
广度优先搜索(BFS)
Breadth-First Search
- 适合搜索最短路径
- 首次找到的一定是最优解(最浅层)
- 空间复杂度高(越深宽度越大,占用内存越多)
快速幂算法
高精度计算的实现
对于每一个数,将其设置为一个bool变量和一个整型数组表示
大整数加法
c++
#include <iostream>
#include <string>
using namespace std;
int main() {
string as, bs;
cin >> as >> bs;
if (as[0] == '+') {
as[0] = '0';
}
if (bs[0] == '+') {
bs[0] = '0';
}
int a[201]{0}, b[201]{0}, c[201]{0};
for (int i = as.size() - 1; i >= 0; i--) {
a[as.size() - 1 - i] = as[i] - '0';
}
for (int i = bs.size() - 1; i >= 0; i--) {
b[bs.size() - 1 - i] = bs[i] - '0';
}
int left = 0;
for (int i = 0; i < 201; i++) {
int temp = a[i] + b[i] + left;
c[i] = temp % 10;
left = temp / 10;
}
bool flag = false;
for (int j = 200; j >= 0; j--) {
if (flag) {
cout << c[j];
}
if (!flag && c[j]) {
flag = true;
cout << c[j];
}
}
if (flag == false) {
cout << 0;
}
return 0;
}大整数减法
c++
大整数乘法
c++
#include <iostream>
#include <string>
using namespace std;
int main() {
string as, bs;
cin >> as >> bs;
int a[201]{0}, b[201]{0}, c[402]{0}; // 增加结果数组的大小
// 将字符串转换为数字数组
for (int i = as.size() - 1; i >= 0; i--) {
a[as.size() - 1 - i] = as[i] - '0';
}
for (int i = bs.size() - 1; i >= 0; i--) {
b[bs.size() - 1 - i] = bs[i] - '0';
}
// 执行乘法运算
for (int i = 0; i < as.size(); i++) {
for (int j = 0; j < bs.size(); j++) {
c[i + j] += a[i] * b[j];
}
}
// 处理进位
for (int i = 0; i < 401; i++) {
if (c[i] > 9) {
c[i + 1] += c[i] / 10;
c[i] %= 10;
}
}
// 找到第一个非零数字
int start = 401;
while (start >= 0 && c[start] == 0) {
start--;
}
// 输出结果
if (start < 0) {
cout << "0";
} else {
for (int i = start; i >= 0; i--) {
cout << c[i];
}
}
return 0;
}大整数除法
c++
#include <stdio.h>
#include <string.h>
#define MAX_LEN 200
char szLine1[MAX_LEN + 10];
char szLine2[MAX_LEN + 10];
int an1[MAX_LEN + 10]; // 被除数, an1[0]对应于个位
int an2[MAX_LEN + 10]; // 除数, an2[0]对应于个位
int aResult[MAX_LEN + 10]; // 存放商,aResult[0]对应于个位
/* Substract 函数:长度为 nLen1 的大整数 p1 减去长度为 nLen2 的大整数 p2
减的结果放在 p1 里,返回值代表结果的长度
如不够减返回-1,正好减完返回 0
p1[0],p2[0] 是个位 */
int Substract(int *p1, int *p2, int nLen1, int nLen2) {
int i;
if (nLen1 < nLen2)
return -1;
// 下面判断 p1 是否比 p2 大,如果不是,返回-1
bool bLarger = false;
if (nLen1 == nLen2) {
for (i = nLen1 - 1; i >= 0; i--) {
if (p1[i] > p2[i])
bLarger = true;
else if (p1[i] < p2[i]) {
if (!bLarger)
return -1;
}
}
}
for (i = 0; i < nLen1; i++) { // 做减法
p1[i] -= p2[i]; // 要求调用本函数时给的参数能确保当 i>=nLen2 时,p2[i] = 0
if (p1[i] < 0) {
p1[i] += 10;
p1[i + 1]--;
}
}
for (i = nLen1 - 1; i >= 0; i--)
if (p1[i])
return i + 1;
return 0;
}
int main() {
int t, n;
char szBlank[20];
scanf("%d", &n);
for (t = 0; t < n; t++) {
scanf("%s", szLine1);
scanf("%s", szLine2);
int i, j;
int nLen1 = strlen(szLine1);
memset(an1, 0, sizeof(an1));
memset(an2, 0, sizeof(an2));
memset(aResult, 0, sizeof(aResult));
j = 0;
for (i = nLen1 - 1; i >= 0; i--)
an1[j++] = szLine1[i] - '0';
int nLen2 = strlen(szLine2);
j = 0;
for (i = nLen2 - 1; i >= 0; i--)
an2[j++] = szLine2[i] - '0';
if (nLen1 < nLen2) {
printf("0\n");
continue;
}
nLen1 = Substract(an1, an2, nLen1, nLen2);
if (nLen1 < 0) {
printf("0\n");
continue;
} else if (nLen1 == 0) {
printf("1\n");
continue;
}
aResult[0]++; // 减掉一次了,商加 1
// 减去一次后的结果长度是 nLen1
int nTimes = nLen1 - nLen2;
if (nTimes < 0) // 减一次后就不能再减了
goto OutputResult;
else if (nTimes > 0) {
// 将 an2 乘以 10 的某次幂,使得结果长度和 an1 相同
for (i = nLen1 - 1; i >= 0; i--) {
if (i >= nTimes)
an2[i] = an2[i - nTimes];
else
an2[i] = 0;
}
}
nLen2 = nLen1;
for (j = 0; j <= nTimes; j++) {
int nTmp;
// 一直减到不够减为止
// 先减去若干个 an2×(10 的 nTimes 次方),
// 不够减了,再减去若干个 an2×(10 的 nTimes-1 次方),......
while ((nTmp = Substract(an1, an2 + j, nLen1, nLen2 - j)) >= 0) {
nLen1 = nTmp;
aResult[nTimes - j]++; // 每成功减一次,则将商的相应位加 1
}
}
OutputResult: // 下面的循环统一处理进位问题
for (i = 0; i < MAX_LEN; i++) {
if (aResult[i] >= 10) {
aResult[i + 1] += aResult[i] / 10;
aResult[i] %= 10;
}
}
// 下面输出结果
bool bStartOutput = false;
for (i = MAX_LEN; i >= 0; i--)
if (bStartOutput)
printf("%d", aResult[i]);
else if (aResult[i]) {
printf("%d", aResult[i]);
bStartOutput = true;
}
if (!bStartOutput)
printf("0\n");
printf("\n");
}
return 0;
}