Home

时间复杂度

一个程序或算法的时间效率, 也称 "时间复杂度" , 有时简称 "复杂度"
复杂度常用大的字母 O 和小写字母 n 来表示, 例如 $O (n)$ , $O (n^{2})$ 等, n 代表问题的规模
时间复杂度是用算法运行过程中, 某种时间固定的操作需要被执行的次数和 n 的关系来度量的, 在无序数列中查找某个数, 复杂度是 $O (n)$
计算复杂度的时候, 只统计执行次数最多的 (n足够大时) 那种固定操作的次数, 例如某个算法需要执行加法 $n^{2}$ 次, 除法 n 次, 那么就记其复杂度是 $O (n^{2})$ 的
复杂度有 "平均复杂度" 和 "最坏复杂度" 两种, 两者可能一致, 也可能不一致
如果复杂度是多个n的函数之和, 则只关心随n的增长, 增长得最快的那个函数
$O(n3 + n 2 ) -> O(n3 ) $
$O(2n + n3) -> O(2n) $
$O (n! + 3 n) - > O (n!)$

常数复杂度: $O (1)$ , 即时间(操作次数)和问题的规模无关
对数复杂度: $O (l o g (n))$
线性复杂度: $O (n)$
多项式复杂度: $O (n^{k})$
指数复杂度: $O (a^{n})$
阶乘复杂度: $O (n!)$

一些例子
在无序数列中查找某个数(顺序查找) $O (n)$
平面上有n个点, 要求出任意两点之间的距离 $O (n^{2})$
插入排序,选择排序,冒泡排序 $O (n^{2})$
快速排序 $O (n * l o g (n))$
二分查找 $O (l o g (n))$

二分查找

BinarySearch
要求是有序区间

例子

写一个函数BinarySeach( ), 在包含size个元素的,从小到大排序的int数组a里如果找到, 则返回元素下标; 如果找不到, 则返回-1, 要求复杂度 $O (l o g (n))$

c++

int BinarySearch(int a[], int size, int p) {
  int L = 0;                   
  int R = size - 1;            
  while (L <= R) {             
    int mid = L + (R - L) / 2;  //为了防止 (L+R)过大溢出
    if (p == a[mid])
      return mid;
    else if (p > a[mid])
      L = mid + 1; 
    else
      R = mid - 1; 
  }
  return -1;
}

写一个函数LowerBound(), 在包含size个元素的,从小到大排序的int数组a里查找比给定整数p小的, 下标最大的元素, 找到则返回其下标, 找不到则返回-1

c++

int LowerBound(int a[], int size, int p) {
  int L = 0;
  int R = size - 1;
  int lastPos = -1;
  while (L <= R) {
    int mid = L + (R - L) / 2;
    if (a[mid] >= p)
      R = mid - 1;
    else {
      lastPos = mid;
      L = mid + 1;
    }
  }
  return lastPos;
}

求下面方程的一个根:$ f(x) = x^3 -5x^2+10x-80 = 0$
若求出的根是 $a$ , 则要求$ |f(a)| <= 10^{-6}$
解法:
对f(x)求导, 得 f'(x)=3x2 -10x+10 由一元二次方程求根公式知, 方程 f'(x)= 0 无解, 因此f'(x)恒大于0 故f(x)是单调递增的易知 f(0) < 0且f(100)>0, 所以区间[0, 100]内必然有且只有一个根由于f(x)在[0, 100]内是单调的, 所以可以用二分法在区间[0, 100]中寻找根

c++

#include <cmath>
#include <cstdio>
#include <iostream>

using namespace std;
double EPS = 1e-6;
double f(double x) { return x * x * x - 5 * x * x + 10 * x - 80; }
int main() {
  double root, x1 = 0, x2 = 100, y;
  root = x1 + (x2 - x1) / 2;
  int triedTimes = 1;
  y = f(root);
  while (fabs(y) > EPS) {
    if (y > 0)
      x2 = root;
    else
      x1 = root;
    root = x1 + (x2 - x1) / 2;
    y = f(root);
    triedTimes++;
  }
  printf("%.8f\n", root);
  printf("%d", triedTimes);
  return 0;
}

输入n (n<= 100, 000)个整数, 找出其中的两个数, 它们之和等于整数m(假定肯定有解), 题中所有整数都能用 int 表示
$s o l u t i o n_{1}$ 双重for循环 $O (n^{2})$
$s o l u t i o n_{2}$ 排序后对于每一个元素二分查找它的配对数 $O (n l o g n)$
$s o l u t i o n_{3}$ 排序后双指针法 $O (n l o g n)$

Aggressive cows
http://bailian.openjudge.cn/practice/2456
农夫John建造了一座很长的畜栏, 它包括N (2≤N≤100, 000)个隔间, 这些小隔间的位置为 $x_{0}, . . ., x_{N - 1} (0 \leq x_{i} \leq 1, 000, 000, 000, 均为整数, 各不相同)$ John的C (2≤C≤N) 头牛每头分到一个隔间, 牛都希望互相离得远点省得互相打扰怎样才能使任意两头牛之间的最小距离尽可能的大, 这个最大的最小距离是多少呢?

c++

#include <algorithm>
#include <iostream>
#include <vector>

using namespace std;
int main() {
  int n, c;
  cin >> n >> c;
  vector<int> location(n, 0);
  for (int i = 0; i < n; i++) {
    cin >> location[i];
  }
  sort(location.begin(), location.end());
  int left = 0, right = location[n - 1] - location[0];
  int last_distance = 0;
  while (left <= right) {
    int distance = left + (right - left) / 2;
    int count = 1;
    int last_pos = location[0];
    for (int i = 0; i < c; i++) {
      auto iter =
          lower_bound(location.begin(), location.end(), last_pos + distance);
      if (iter != location.end()) {
        count++; 
        last_pos = *(iter);
      } else {
        right = distance - 1;
        break;
      }
      if (count == c) {
        left = distance + 1;
        last_distance = distance;
        break;
      }
    }
  }
  cout << last_distance << endl;
  return 0;
}

枚举

找到解空间
- 模型中变量数尽可能少, 它们之间相互独立
缩小解空间
- 利用知识缩小模型中各变量的取值范围, 避免不必要的计算
使用合适的搜索顺序遍历
- 搜索空间的遍历顺序要与模型中条件表达式一致

例题

题目描述 $a^{3} = b^{3} + c^{3} + d^{3}$ 为完美立方等式.例如 $12^{3} = 6^{3} + 8^{3} + 10^{3}$ .编写一个程序,对任给的正整数N (N≤100),寻找所有的四元组(a, b, c, d),使得 $a^{3} = b^{3} + c^{3} + d^{3}$ ,其中1<a, b, c, d ≤N.
输入正整数N (N≤100)
输出每行输出一个完美立方,按照a的值,从小到大依次输出.当两个完美立方等式中a的值相同,则依次按照b,c,d进行非降升序排列输出,即b值小的先输出,然后c值小的先输出,然后d值小的先输出.
样例输入
24
1
样例输出
Cube = 6, Triple = (3,4,5)
Cube = 12, Triple = (6,8,10)
Cube = 18, Triple = (2,12,16)
Cube = 18, Triple = (9,12,15)
Cube = 19, Triple = (3,10,18)
Cube = 20, Triple = (7,14,17)
Cube = 24, Triple = (12,16,20)
1
2
3
4
5
6
7

c++

描述人生来就有三个生理周期,分别为体力周期,感情周期和智力周期,它们的周期长度分别为23天,28天和33天.每一个周期中有一天是高峰.在高峰这天,人会在相应的方面表现出色.例如,在智力周期的高峰,人会思维敏捷,注意力容易高度集中.因为三个周期的长度不同,所以通常三个周期的高峰不会落在同一天.对于每个人,想知道何时三个高峰落在同一天.对于每个周期,会给出从当前年份的第一天开始,到出现高峰的天数(不一定是第一次高峰出现的时间).给定一个从当年第一天开始的天数,你的任务是输出从给定时间开始(不包括给定时间),下一次三个高峰落在同一天的时间(距给定时间的天数).例如:给定时间为10,下次出现三个高峰同一天的时间是12,则输出2(注意这里不是3).
输入输入包含多组数据,每一组数据由四个整数组成,数据以-1 -1 -1 -1 结束. 对于四个整数p, e, i和d,p, e, i分别表示体力,情感和智力高峰出现的时间(时间从当年的第一天开始计算).d是给定的时间,可能小于p, e或i.所有给定时间是非负的并且小于或等于365,所求的时间小于或等于21252.
输出从给定时间起,下一次三个高峰同一天的时间(距离给定时间的天数).
样例输入
0 0 0 0
0 0 0 100
5 20 34 325
4 5 6 7
283 102 23 320
203 301 203 40
-1 -1 -1 -1
1
2
3
4
5
6
7
样例输出
Case 1: the next triple peak occurs in 21252 days.
Case 2: the next triple peak occurs in 21152 days.
Case 3: the next triple peak occurs in 19575 days.
Case 4: the next triple peak occurs in 16994 days.
Case 5: the next triple peak occurs in 8910 days.
Case 6: the next triple peak occurs in 10789 days.
1
2
3
4
5
6

c++

问题描述 有12枚硬币.其中有11枚真币和1枚假币.假币和真币重量不同,但不知道假币比真币轻还是重.现在,用一架天平称了这些币三次,告诉你称的结果,请你找出假币并且确定假币是轻是重,数据保证一定能找出来.
输入样例
ABCD EFGH even
ABCI EFJK up
ABIJ EFGH even
1
2
3
输出样例
K it is light.
1

c++

题目描述有一个由按钮组成的矩阵,其中每行有6个按钮,共5行.每个按钮的位置上有一盏灯.当按下一个按钮后,该按钮以及周围位置(上边,下边,左边,右边)的灯都会改变一次.即,如果灯原来是点亮的,就会被熄灭;如果灯原来是熄灭的,则会被点亮.在矩阵角上的按钮改变3盏灯的状态;在矩阵边上的按钮改变4盏灯的状态;其他的按钮改变5盏灯的状态.
在上图中,左边矩阵中用X标记的按钮表示被按下,右边的矩阵表示灯状态的改变.对矩阵中的每盏灯设置一个初始状态.请你按按钮,直至每一盏等都熄灭.与一盏灯毗邻的多个按钮被按下时,一个操作会抵消另一次操作的结果.在下图中,第2行第3,5列的按钮都被按下,因此第2行,第4列的灯的状态就不改变.
请你写一个程序,确定需要按下哪些按钮,恰好使得所有的灯都熄灭.根据上面的规则,我们知道1)第2次按下同一个按钮时,将抵消第1次按下时所产生的结果.因此,每个按钮最多只需要按下一次;2)各个按钮被按下的顺序对最终的结果没有影响;3)对第1行中每盏点亮的灯,按下第2行对应的按钮,就可以熄灭第1行的全部灯.如此重复下去,可以熄灭第1,2,3,4行的全部灯.同样,按下第1,2,3,4,5列的按钮,可以熄灭前5列的灯.
输入 5行组成,每一行包括6个数字(0或1).相邻两个数字之间用单个空格隔开.0表示灯的初始状态是熄灭的,1表示灯的初始状态是点亮的.
输出 5行组成,每一行包括6个数字(0或1).相邻两个数字之间用单个空格隔开.其中的1表示需要把对应的按钮按下,0则表示不需要按对应的按钮.
样例输入
0 1 1 0 1 0
1 0 0 1 1 1
0 0 1 0 0 1
1 0 0 1 0 1
0 1 1 1 0 0
1
2
3
4
5
样例输出
1 0 1 0 0 1
1 1 0 1 0 1
0 0 1 0 1 1
1 0 0 1 0 0
0 1 0 0 0 0
1
2
3
4
5

c++

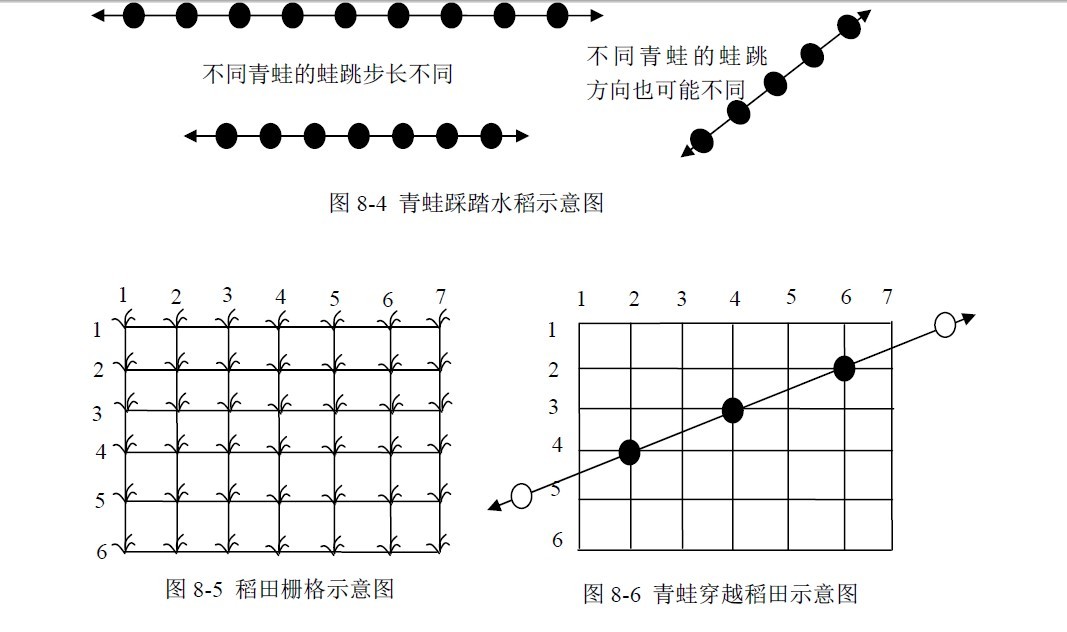
问题描述 在韩国,有一种小的青蛙.每到晚上,这种青蛙会跳越稻田,从而踩踏稻子.农民在早上看到被踩踏的稻子,希望找到造成最大损害的那只青蛙经过的路径.每只青蛙总是沿着一条直线跳越稻田,而且每次跳跃的距离都相同,如图8-4 所示. 稻田里的稻子组成一个栅格,每棵稻子位于一个格点上,如图8-5 所示.而青蛙总是从稻田的一侧跳进稻田,然后沿着某条直线穿越稻田,从另一侧跳出去,如图8-6 所示.
青蛙的每一跳都恰好踩在一棵水稻上,将这棵水稻拍倒.可能会有多只青蛙从稻田穿越, 有些水稻被多只青蛙踩踏,如图8-7 所示.当然,农民所见到的是图8-8 中的情形,看不到图8-7中的直线.
根据图8-8,农民能够构造出青蛙穿越稻田时的行走路径,并且只关心那些在穿越稻田时至少踩踏了3 棵水稻的青蛙.因此,每条青蛙行走路径上至少包括3 棵被踩踏的水稻.而在一条青蛙行走路径的直线上,也可能会有些被踩踏的水稻不属于该行走路径.在图8-8 中, 格点(2, 1),(6, 1)上的水稻可能是同一只青蛙踩踏的,但这条线上只有两棵被踩踏的水稻, 因此不能作为一条青蛙行走路径;格点(2, 3),(3, 4),(6, 6)在同一条直线上,但它们的间距不等,因此不能作为一条青蛙行走路径;格点(2, 1),(2, 3),(2, 5),(2, 7)是一条青蛙行走路径,该路径不包括格点(2, 6).请你写一个程序,确定在所有的青蛙行路径中,踩踏水稻棵数最多的路径上有多少棵水稻被踩踏.例如,图8-8 的答案是7,因为第6 行上全部水稻恰好构成一条青蛙行走路径. 输入数据 从标准输入设备上读入数据.第一行上两个整数R,C,分别表示稻田中水稻的行数和列数,1≤R,C≤5000.第二行是一个整数N,表示被踩踏的水稻数量, 3≤N≤5000.在剩下的N 行中,每行有两个整数,分别是一颗被踩踏水稻的行号(1~R)和列号(1~C),两个整数用一个空格隔开.而且,每棵被踩踏水稻只被列出一次. 输出要求 从标准输出设备上输出一个整数.如果在稻田中存在青蛙行走路径,则输出包含最多水稻的青蛙行走路径中的水稻数量,否则输出0. 输入样例
6 7
14
2 1
6 6
4 2
2 5
2 6
2 7
3 4
6 1
6 2
2 3
6 3
6 4
6 5
6 7
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
输出样例
7
1

c++

递归

某个函数直接或间接的调用自身
问题的求解过程 :
- 划分成许多相同性质的求解
- 小问题的求解过程可以很容易的求出
- 这些子问题的解就构成原问题的解
递归的基本思想
- 待求解问题的解输入变量x的函数f (x)
- 通过寻找函数 g( ), 使得f (x) = g(f (x-1))
- 且已知f(0) 的值, 就可以通过f(0) 和g( ) 求出f(x)的值
推广
- 扩展到多个输入变量x, y, z等, x-1也可以推广到 x - x1
- 只要递归朝着 "出口" 的方向即可

递归和枚举的区别

枚举

把一个问题划分成一组子问题, 依次对这些子问题求解

子问题之间是横向的同类的关系

递归

把一个问题逐级分解成子问题

子问题与原问题之间是纵向的同类的关系

语法形式上:在一个函数的运行过程中, 调用这个函数自己

-　直接调用: 在fun()中直接执行fun()

-　间接调用: 在fun1()中执行fun2();在fun2()中又执行fun1()

递归的3个要素

递归表达式
- 如何将原问题划分成子问题
递归终止的条件
- 即最小子问题的求解, 可以允许多个出口
界函数
- 问题规模变化的函数, 它保证递归的规模向出口条件靠拢

例题

给定n,求解n的阶乘

c++

int Factorial(int n){
	if (n == 0){
        return 1;
    }
	else{
        return n*Factorial(n-1);
	}	
}

POJ2000 金币
描述国王将金币作为工资,发放给忠诚的骑士.第一天,骑士收到一枚金币;之后两天(第二天和第三天)里,每天收到两枚金币;之后三天(第四,五,六天)里,每天收到三枚金币;之后四天(第七,八,九,十天)里,每天收到四枚金币...这种工资发放模式会一直这样延续下去:当连续N天每天收到N枚金币后,骑士会在之后的连续N+1天里,每天收到N+1枚金币(N为任意正整数).
你需要编写一个程序,确定从第一天开始的给定天数内,骑士一共获得了多少金币.
输入输入包含至少一行,但不多于21行.除最后一行外,输入的每行是一组输入数据,包含一个整数(范围1到10000),表示天数.输入的最后一行为0,表示输入结束.
输出对每个数据输出一行,包含该数据对应天数和总金币数,用单个空格隔开.
样例输入
10
6
7
11
15
16
100
10000
1000
21
22
0
1
2
3
4
5
6
7
8
9
10
11
样例输出
10
6 14
7 18
11 35
15 55
16 61
100 945
10000 942820
1000 29820
21 91
22 98
1
2
3
4
5
6
7
8
9
10
来源 Rocky Mountain 2004

c++

#include <iostream>
using namespace std;
int getCoins(int pay, int days) {
  if (days <= pay) {
    return pay * days;
  }
  return pay * pay + getCoins(pay + 1, days - pay);
}
int main() {
  int n;
  while (scanf("%d", &n)) {
    if (n == 0)
      break;
    printf("%d %d\n", n, getCoins(1, n));
  }
  return 0;
}

$d a y s = \frac{n * (n - 1)}{2}$

$n^{2} - n - 2 * d a y s = 0$

c++

POJ2694逆波兰表达式

原题:
问题描述:
逆波兰表达式是一种吧运算符前置的算术表达式,例如普通的表达式2+3的逆波兰表示为+23.逆波兰表达式的优点是运算符之间不必有优先级的关系,也不必有括号改变运算次序,例如(2+3)4的逆波兰表示法为+2 3 4.本题求解的逆波兰表达式的值.
输入数据:
输入为一行,其中运算符和运算数之间都用空格分隔,运算数是浮点数.
输出要求:
输出为一行,即表达式的值.
输入样例:
* + 11.0 12.0 + 24.0 35.0
1
输出样例:
1357.000000
1

c++

逆波兰表达式翻译为一般表达式

c++

常规表达式的计算

c++

POJ1191 棋盘分割
积分图

c++

POJ1390

c++

当前的学习重心

归档

ai

language

general_psychology

hpc

other

program

data_algorithm

时间复杂度

二分查找

例子

枚举

例题

递归

递归和枚举的区别

递归的3个要素

例题

POJ2694逆波兰表达式

动态规划

ai

language

general_psychology

hpc

other

program

data_algorithm

时间复杂度 ​

二分查找 ​

例子 ​

枚举 ​

例题 ​

递归 ​

递归和枚举的区别 ​

递归的3个要素 ​

例题 ​

POJ2694逆波兰表达式 ​

动态规划 ​

时间复杂度

二分查找

例子

枚举

例题

递归

递归和枚举的区别

递归的3个要素

例题

POJ2694逆波兰表达式

动态规划